道可道，非常道；名可名，非常名。
无名，天地之始，有名，万物之母。
故常无欲，以观其妙，常有欲，以观其徼。
此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

本笔记仅记录本人没学过的东西

基础知识

序列

序列指的是把对象按照一定的次序列举出来。可以是有限的，可以是无限的；可以由递归定义一个序列，也可以显式定义一个序列。

如果$A\subseteq U$，对$\forall x \in A$，$A$上的特征函数$f_A$定义为

$f_A(x)=\begin{cases} 1,&x\in A\\ 0,&x\not\in A \end{cases}$

有$f_{A\cap B}=f_A \& f_B$（集合并等于特征函数位并），类似的可以列出其他位运算成立的式子。

如果一个集合是有限集，则其特征函数可以使用序列来表示（计算机表示）（离散化）。

串与正则表达式

已知集合$A$，可以构造由$A$中所有有限序列所组成的集合$A^*$。$A$被称为字母表，$A^*$中的所有元素称作$A$中的字或者字符串，用$\Lambda$表示空字符串。

如果对于$w_1=s_1s_2\cdots s_n,w_2=t_1t_2\cdots t_n.w_1,w_2\in A^*$，定义$w_1$与$w_2$的连接为序列$s_1s_2\cdots s_nt_1t_2\cdots t_n$，记作$w_1\cdot w_2$或$w_1w_2$。显然其也在$A^*$中。

由以下规则递归构造$(\{x|x\in A\}\land\{(,),\land,*,\lor\})^*$的字符串，称其为$A$上的正则表达式$re$

$\begin{aligned} \text{RE1}:\space &符号\Lambda 是正则表达式。 \\ \text{RE2}:\space &如果x\in A，则x是正则表达式。 \\ \text{RE3}:\space &如果\alpha 和 \beta 是正则表达式，则\alpha\beta 是正则表达式。 \\ \text{RE4}:\space &如果\alpha 和 \beta 是正则表达式，则\alpha\lor\beta 是正则表达式。 \\ \text{RE5}:\space &如果\alpha 是正则表达式，则(\alpha)^*是正则表达式。 \end{aligned}$

定义$G(re)$为按照以下规则递归构造出的字符串集合

$\begin{aligned} 1.\space &G(\Lambda)=\{\Lambda\} \\ 2.\space &如果x\in A，则G(x)=\{x\} \\ 3.\space &如果\alpha 和 \beta 都是A上的正则表达式，则G(\alpha\beta)=\{s\in G(\alpha),t\in G(\beta)|st\} \\ 4.\space &如果\alpha 和 \beta 都是A上的正则表达式，则G(\alpha \lor \beta)=G(\alpha)\lor G(\beta) \\ 5.\space &如果\alpha是A上的正则表达式，则G((\alpha)^*)=G(\alpha)^* \end{aligned}$

正则表达式的匹配就是判断一个字符串是否在其$G$函数表示的集合内。

数学结构

我们称对于某个集合，定义了其元素的一些运算。集合和这些运算构成了一个数学结构，用$(集合,+,-)$来表示，比如$(R,+,-,*,/)$。

只有一个操作数的运算是一元运算，结合两个操作数的运算是二元运算。

如果一个数学结构里运算的结果仍然在集合中，我们称这个结构关于这个运算是封闭的。

对于一个集合$A$上的一个二元运算$\odot$

我们称其是可交换的当且仅当$\forall x,y\in A\space ,A\odot B=B\odot A$

我们称其是可结合的当且仅当$\forall x,y,c\in A\space ,(A\odot B)\odot C=A\odot (B\odot C)$

左结合性指同等优先级的表达式在不加括号的情况下，从左至右执行。$+,-,*,/$都是左接合的。

对于一个集合$A$上的两个二元运算$\odot$和$\oplus$，我们称$\odot$对$\oplus$可分配当且仅当$\forall x,y,c\in A\space ,A\odot (B\oplus C)=(A\odot B)\oplus (A\odot C)$。

如果对于一个二元运算$\odot$，$\exist e,\forall x \in A,x\odot e=e\odot x=e$。我们称$e$是$\odot$的一个单位元。一个二元运算的单位元一定唯一。

如果一个二元运算$\odot$存在单位元$e$，如果$x,y \in A,x\odot y=y\odot x=e$。我们称$y$是$x$的逆。

逻辑

命题是或者为真或者为假而不是两者同时成立的一条陈述语句。

命题变量出现在命题中，能以$命题$代替。命题或命题变量能通过逻辑联结词接合获得复合命题。

在自然语言中，a或b有两种意思。一种是a和b只能有一个为真，一种是a和b有一个为真。逻辑中或只有后者的意思，所以需要结合语境来转换自然语言描述的命题。

如果$p$和$q$是命题，$p$和$q$的析取是复合命题”$p$或$q$“，用$p\lor q$来表示。折取用$p\land q$来表示。

定义命题函数为从定义域里的元素产生命题的函数$\text P(x)$，也叫谓词。

$\text P(x)$的全称量化是命题"对于所有$x$的值，$\text P(x)$为真"，用$\forall x\space\text P(x)$表示，$\forall$称为全称量词。

$\text P(x)$的存在量化是命题"存在一个$x$，$\text P(x)$为真"，用$\exist x\space\text P(x)$表示，$\exist$称为存在量词。

如果$p$和$q$是命题，那么复合命题“如果$p$，那么$q$”称为条件命题或蕴含，用$p\Rightarrow q$表示，$p$称为前项或假设，$q$称为后项或结论。蕴含关系的真值表如下

$p$	$q$	$p\Rightarrow q$
T	T	T
T	F	F
F	T	T
F	F	T

相比自然语言，逻辑中蕴含用在更弱的意义下。

命题变量所有的可能值都为真的命题称为重言式。总是为假的命题称为矛盾或者谬论；命题的真假依赖于命题变量的真值，这种命题称为不定式。

若$p\Leftrightarrow q$是重言式，可以说$p$和$q$是逻辑等价的，或者简称等价。

证明方法

如果$p\Rightarrow q$是一个重言式，那么称从$p$逻辑上得到q，这里$p$和$q$可以是包含许多命题变量的复合命题，如$(p_1\land p_2\land \cdots \land p_n)\Rightarrow q$是重言式，此时称从$p_1\land p_2\land \cdots \land p_n$逻辑上得到$q$，记为

$p_1 \\ p_2 \\ \vdots \\ p_n \\ \overline{\therefore q}$

$p_i$称为假设或前提，$q$称为结论。基于重言式的论证称为推理规则。以下是一些重要的推理规则。

$p \\ p\Rightarrow q\\ \overline{\therefore q}$

此为假言推理

$p \\ (\sim q)\Rightarrow(\sim p) \\ \overline{\therefore q}$

此为间接方法

$p\Rightarrow q \\ \sim q \\ \overline{\therefore\space \sim p}$

此为反证法

数学归纳法

想证明$\forall n\ge n_0\space P(n)$，其中$n$为整数，只需证明$P(n_0)\land (\forall m\ge n,\space \text P(m)\Rightarrow\text P(m+1))$为真即可。可写出以下步骤。

$\begin{aligned} &\qquad\bold{基础步骤}\space .......\\ &\qquad \bold{归纳步骤}\space ....... \\ &由数学归纳法得到，\text P(n)对于所有的n\ge 1为真。 \end{aligned}$

强形式的数学归纳法或强归纳法是证明$\def \P {\text{P}} \P(n_0)\land \P(n_0+1)\land \P(n_0+2)\land \cdots\land \P(k)\Rightarrow \P(k+1)$是一个重言式。基本步骤和前面一样。

强归纳和归纳法等价

计数

如果递归关系具有以下形式

$a_n=\sum_{i=1}^k r_ka_{n-k}$

其中$r_i$为常数，称其是$\bold{k}$阶线性其次关系。其有特征方程$x^k=\sum_{i=0}^kr_1x^{k-1}$。对于2阶线性其次递归关系，其特征方程的根和递归关系的显式公式如下

$\begin{aligned} 有两个根s_1,s_2时，&a_n=us^n+vs_2^n\\ 有一个根s时，&a_n=us^n+vns^n \end{aligned}$

关系和有向图

关系

定义集合上的笛卡尔积$A_1\times A_2\times\cdots\times A_n =\{(a_1,a_2,\cdots,a_n)|a_i\in A_i,i=1,2,\cdots,m\}$

右式表达的元素称为有序m-元。

一个物件有$n$个属性，属性的值就构成了这个属性的集合$A_i$。

一个关系型数据库$D$是$A_1\times A_2\times\cdots\times A_n$的一个子集，其中每个$A_i$标识一个数据的属性，一个属性称为一个关键字。

设$A,B$为非空集合，从$A\bold{到}B\bold{的一个关系}R$是$A\times B$的一个子集。如果$R\subseteq A\times B$且$(a,b)\in R$，我们称$a\bold与b\bold是R\bold{相关的}$，记为$a\ R\ b$，如果不是，则记为$a\ \not R\ b$，通常$A=B$，则往往称$R\bold是A上\bold{的一种关系}$。

比如集合{1,2,3}到集合{4,5,6}的一个关系R={{2,4},(3,6)}

$R$的定义域用$\text{Dom}(R)$表示，$\text{Dom}(R)\in A$。$R$的值域用$\text{Ran}(R)$表示，$\text{Ran}(R)\in B$。

如$x\in A$,记$R(x)=\{y\in B| x\ R\ y\}$

如$A_1\subseteq A$记$R(x)=\{y\in B| \exist x\in A_1,x\ R\ y\}$

如$A=\{a_1,\cdots,a_n\},B=\{b_1,\cdots,b_n\}$，$R$是从$A$到$B$的一个关系，定义$R$的矩阵$M_R=[m_{ij}],m_{i,j}=\begin{cases}1,\quad(a_i,b_j)\in R\\0,\quad Others \end{cases}$。

如果$A$是个有限集，$R$是$A$上的关系。可将$A$的元素看成点，每个$x\in R$看成单向边，构成了一个有向图，称为$R$的有向图。

定义$x\ R^n\ y$指存在$a_1,\cdots,a_{n-1}$使得$n$个关系$x\ R\ a_1,a_1\ R\ a_2,\cdots,a_{n-1}\ R\ y$成立。（路径）

$R^k$也是一个关系

定义$x\ R^\infty\ y$指存在$k$，使得$x\ R^k\ y$成立。（连通）

有$M_{R^2}=M_R\odot M_R$（布尔积）

关系的性质

称关系$R$是自反的，当且仅当$\forall a\in A,有a\ R\ a$。

称关系$R$是非自反的，当且仅当$\forall a\in A,有a\ \not R\ a$。

称关系$R$是对称的，当且仅当$\forall a\ R\ b则b\ R\ a$。（无向）

称关系$R$是非对称的，当且仅当$\forall a\ R\ b则b\ \not R\ a$。（单向，无自环）

称关系$R$是反对称的，当且仅当如$\forall a\ R\ b\land b\ R\ a$则$a=b$。（单向，不care自环有无）

称关系$R$是传递的，当且仅当$\forall a\ R\ b\land b\ R\ c$则$a\ R\ c$。

等价关系

如果$R$是自反的、对称的和传递的，称其是一个等价关系。

等价关系的有向图是一个包含有几个完全图的图

关系运算

下文中所有关系均设为集合$A$上。

关系是集合，可以用集合运算。

$a\ R^{-1}\ b$当且仅当$b\ R\ a$。（逆）

有以下关系运算后自反性质的定理

• 如$R$自反，则$R^{-1}$自反
• 如$R$和$S$自反，则$R\cap S$和$R\cup S$是自反
• $R$自反当且仅当$\overline R$是非自反（补集）

有以下关系运算后对称性质的定理

• $R$是对称的当且仅当$R=R^{-1}$
• $R$是反对称的当且仅当$R\cap R^{-1}\subseteq \Lambda$（$\Lambda=\{a\in A|(a,a)\}$）
• $R$是非对称的当且仅当$R\cap R^{-1}=\emptyset$

有以下关系运算后的定理

• $(R\cap S)^2\subseteq R^2\cap S^2$
• 如$R$和$S$都是传递的，则$R\cap S$是传递的
• 如$R$和$S$都是等价的，则$R\cap S$是等价的

闭包

我们希望从集合上的一个关系$R$出发，向$R$添加一些对，使其满足某些性质。如果存在最小关系$R_1$，称其是关于该性质的$R$的闭包。

$R$的自反闭包是$R\cup \Lambda$；$R$的对称闭包是$R\cup R^{-1}$；$R$的传递闭包是$R^\infty$。

如果$R$是$A$到$B$的关系，$S$是$B$到$C$的关系，称$R$和$S$的合成为$\{(a,b)\in R,(b,c)\in S|(a,c)\}$，记为$S\circ R$。

有$M_{S\circ R}=M_R \odot M_S$

有$R^\infty=\bigcup_{n=1}^\infty R^n$，如果$|A|=n$，退化为$R^\infty=\bigcup_{i=1}^n R^i$。

$Floyd-Warshall$算法如下

设$R$是$集合A={a_1,a_2,\cdots,a_n}$上的一个关系，如果$x_1,x_2,\cdots,x_m$是$R$中的一条道路，除了$x_1\cdots x_m$以外的任何顶点都称作道路的内顶点。定义布尔矩阵$W_k$如下，$W_k[i,j]$为$1$当且仅当$R$中存在$a_i$到$a_j$的一条道路，它的内顶点构成的集合是$\{a_1,\cdots,a_k\}$的子集。

不妨设$W_0=M_R$，有$W_n=M_{R^\infty}$。

利用动态规划的思想，得到

$W_{k}[i,j]= \begin{cases} 1,\quad W_{k-1}[i,j]=1\ \lor (W_{k-1}[i,k]=1\land W_{k-1}[k,j]=1) \\ 0,\quad others\\ \end{cases}$

时间复杂度$O(n^3)$。

序关系和序结构

如果某个集合$A$上的关系$R$是自反的、反对称的和传递的，称$R$是一个偏序。集合$A$与偏序$R$一起称作偏序集$(A,R)$。（DAG）

$(A,R^{-1})$是$(A,R)$的对偶，$R^{-1}$是$R$的对偶。

如果$a\ R\ b\lor b\ R\ a$成立称$a,b$可比。如果$\forall a,b \in A\ a,b$可比成立，称$A$是一个全序，也称$A$是一个链。（此处应有std::sort）

如果$(A,\le)$和$(B,\le)$是偏序集，则$(A\times B,\le)$是偏序集，如果$(a,b)\le (a',b')$，当且仅当$a\le a'\land b\le b'$。称笛卡尔积上的这种偏序为积偏序。

如果$(A,\le)$和$(B,\le)$是偏序集，则$(A\times B,\prec)$是偏序集，如果$(a,b)\prec (a',b')$，当且仅当$a<a' \lor (a=a'\land b< b)'$。称笛卡尔积上的这种偏序为字典序。
（std::pair，std::tuple，std::string，std::array）

哈塞图是一种表示偏序集的特殊无向图。其表示了一个每条边的方向都是从下往上，忽略了自环的和路径长度大于1的有向图。这个有向图就是偏序集关于这个关系的有向图。

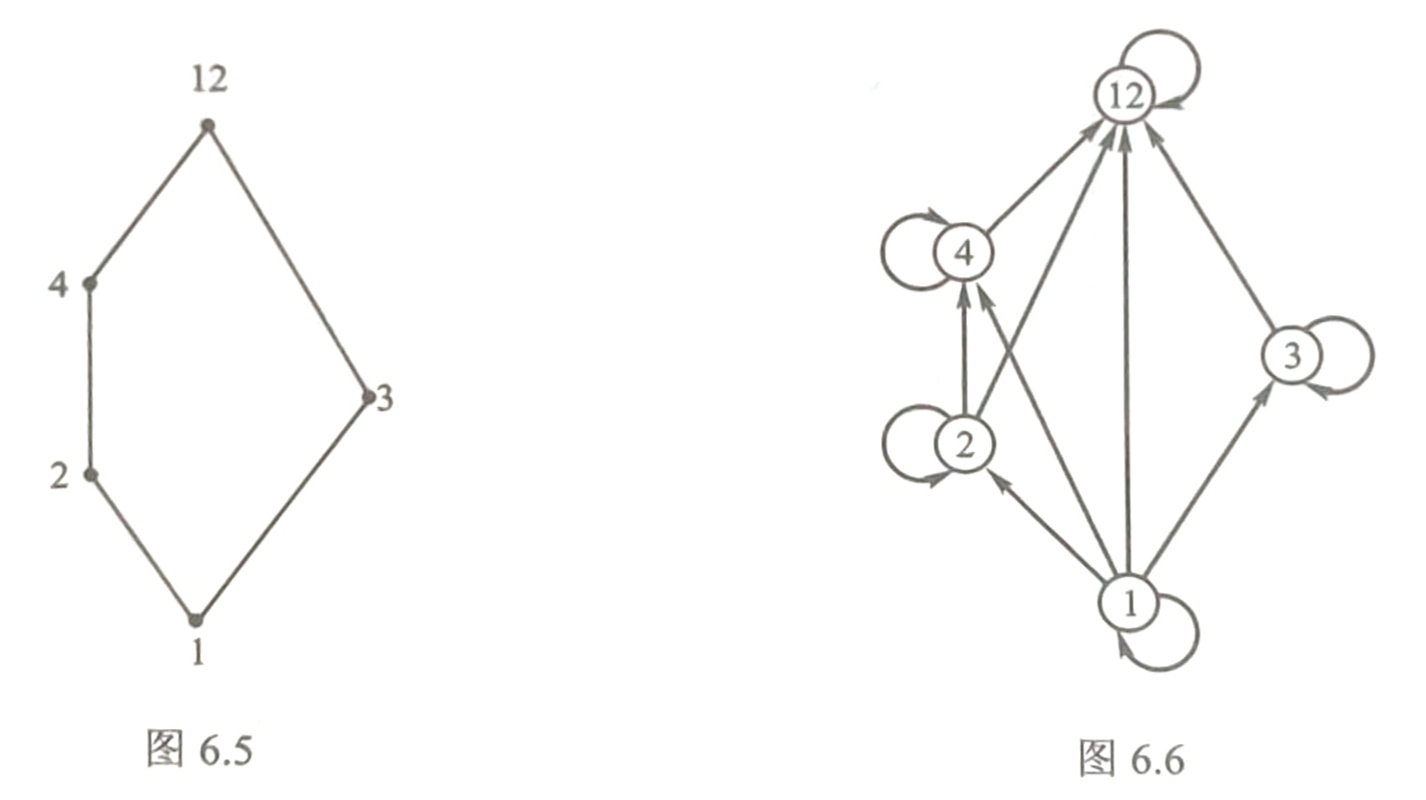
拓扑排序就是DAG的一个可能的搜索路径。

设$(A,R)$和$(A',R')$是偏序集，如果存在一个双射$f:\ A\rightarrow A'$，使得$\forall a ,b\in A\ ,a\ R\ b\Leftrightarrow f(a)\ R'\ f(b)$，则称函数$f$是从$(A,R)$到$(A',R')$的一个同构，称$(A,R)$和$(A',R')$是同构的偏序集。

极小元指的是哈塞图中的所有DAG起点，极大元指的是哈塞图中所有DAG终点。最大元$a$满足$\forall x\in A,x\ R\ a$成立，最小元$a$满足$\forall x\in A,x\ R^{-1}\ a$成立。

$B\subset A$的上界$\text{LUB}(B)$指的是$B$集合的所有公共祖先，下界$\text{GLB}(B)$指的是$B$集合的所有公共孩子。最小上界是唯一的最小公共祖先，最小下界是唯一的最大公共孩子。（草）

格

格是A的一个子集$A'$，满足$\forall a,b\in A'\ ,\exist \text{LUB}(\{a,b\}),\exist \text{GLB}(\{a,b\})$。