2021新生赛题目&std数据&题解（爱丽丝的玩偶、答案在天空、这里没有数据结构）.zip

链接: https://pan.baidu.com/s/1kPaqACI9dUGIksKFiMERnQ 提取码: k3fr

以下是在线版，仅有题目std题解，公式包含一些渲染问题。

爱丽丝的人偶

题面

题目背景

我们仍未知道爱丽丝的人偶是如何制作的。不过巫女也不关心正直者们的死活，爱丽丝的人偶谜团或许永远都不会揭晓。

恰逢春雪异变结束，等待了许久的春天终于到来。在春雪异变跟爱丽丝的弹幕决斗时，爱丽丝操纵人偶战斗给魔理沙留下了深刻的印象。魔理沙决定拿几个人偶研究研究，不过爱丽丝的人偶都有自主意识，魔理沙的各种拿人偶攻势均以失败告终。

迫于无奈，爱丽丝终于同意送给魔理沙一个人偶，但是在此之前他想考验一下魔理沙。如果魔理沙答错的话，爱丽丝可就要将偷人偶的仇融入在她和梅蒂欣共同研发的试做型剧毒人偶中送给魔理沙。据说这玩偶的毒在魔法森林中心完全释放出来能令整个魔法森林寸草不生。

魔理沙，大危机！

题目描述

爱丽丝有$n$个人偶站成一排队伍，从左到右编号为$\{0,1,2,3,..,n-3,n-2,n-1\}$。爱丽丝让人偶们从左到右开始报数，如果有人偶报数是奇数，则立即离开队伍。报完数之后爱丽丝继续让人偶队伍这样报数，直到队伍中没有人偶。爱丽丝问魔理沙第$q$个离开队伍的人偶的编号是多少？

输入格式

一行以空格分割的两个整数$n,q$

输出格式

一行一个数字，表示第$q$个离开队伍的人偶编号

样例1

输入

10 1

输出

0

样例2

输入

10 7

输出

5

数据范围

$1 \le q\le n \le 10^{18}$

题解

设当前队伍玩偶数为$n$

• 命题0：整个队伍报道完成一次有$\lceil n/2\rceil$个玩偶离开队伍，队伍里还剩下$\lfloor n/2 \rfloor$个玩偶。

显然

• 命题1：整个队伍第$i$次完成报数时，离开队伍的玩偶的编号形成一个公差为$2^i$的等差数列；队伍中剩下的玩偶的编号形成一个公差为$2^i$的等差数列

显然

• 命题2：整个队伍第$i$次完成报数时，离开队伍的玩偶的编号的二进制表达中第$i$位为0，第$1..i-1$位为1，队伍中剩下的玩偶的编号的二进制表达中第$1..i$位为1

归纳法证明，$i=1$时显然

设$i=n-1$时原命题成立

离开队伍的玩偶的编号的二进制表达中第$n-1$位为0，第$1..n-2$位为1，队伍中剩下的玩偶的编号的二进制表达中第$1..n-1$位为1

命题1有效，队伍中剩下的玩偶的编号形成一个公差为$2^{n-1}$的等差数列

下证$i=n$时原命题成立

第$n$次报到前队伍中的玩偶应该为\{x|j\cross 2^{n-1}+(2^{n-1}-1),j\in Z \land j\ge 0\}

第$n$次报到后离开的玩偶编号应该为\{x|2\cross j\cross 2^{n-1}+(2^{n-1}-1),j\in Z \land j\ge 0\}

即\{x|j\cross 2^{n}+(2^{n-1}-1),j\in Z \land j\ge 0\}，显然其二进制表达中第$1..n-1$位为1，第$n$位为0。同理对队伍中剩下的玩偶原命题成立。所以原命题成立。

• 表达式1：所以第$i$轮中第$j$个离开的玩偶的编号为(j-1)\cross 2^{i}+(2^{i-1}-1)

又根据命题0，则只需循环模拟轮数，直到第$i$轮包括了请求的第$x$个离开的玩偶，应用表达式1即可计算答案。

时间复杂度$O(log n)$

std

#include <bits/stdc++.h>

using namespace std;

int main(){
	unsigned long long n,q;int i=0;
	cin>>n>>q;
	while (true){
		auto wq=(n+1)/2;
		if (q<=wq) break;
		n-=wq;
		q-=wq;
		i++;
	}
	unsigned long long a=(1ull<<i)-1,b=(1ull<<(i+1));
	cout << a+b*(q-1) << endl;
}

遥望远方，答案就在天空的那一端！

题面

题目背景

小时候，我无所畏惧。

那时，我觉得自己有无限的可能性，不会输给任何人，能去到任何我想去的地方。

这个世界无限广阔，而我只要稍稍蹒起脚尖,就能够将它尽收眼底。

我要做的,只是向天空伸出手。

「你就没有感到很受挫的时候吗?」

「拿FC来举例的话，就是在输了比赛，或者在训练中无法随心所欲地飞的时候。人只要活着，就会有感到挫折的时候」

「你在这种时候不会陷入烦恼或者失落吗?」

「我和她约好，要一直努力向上、加油进步、保持乐观开朗，还有，对待喜欢的事物要一心一意」

「后来我发现，只要这样保持下去,我的缺点就能改正」

「所以，我默默决定了，唯独在坚持不懈这点上我决不能输给任何人」

「...…我却拒绝了那片天空」

「我不希望明日香也留下和我一样的回忆」

「我希望你能一直保持着第一眼见到这片天空的时的感动，自由自在地飞翔」

「——仰望天空，注视天空，答案就在那里」

「没事」

「——这样已经足够了」

题目描述

凭借着反重力粒子靴，人们能无视地球重力的影响飞行，因此诞生了一项在空中飞行的体育运动——Flying Circus。

Flying Circus比赛中会设立一个足够高的标记，所有运动员都得从这个标记起飞，所有高度都需要用相对于标记的高度表示，叫做相对高度。

仓科明日香是一名Flying Circus选手，她有一个叫做空中回弹的绝招，允许她朝着空气中存在的重力粒子快速移动。她想试试只使用空中回弹自己能飞到多高。

现在明日香在相对高度为$a$的位置上，她的正上方和正下方漂浮着$n$个相对高度为$h_i$的重力粒子（$h_i\ne 0$且两两不相等）。如果明日香当前相对高度为$x$，使用了一个相对高度为$h$的重力粒子进行空中回弹，那么明日香会瞬间飞往高度$y$，$x$和$y$关于$h$对称。比如明日香当前相对高度为$4$，使用相对高度为$-2$的重力粒子进行空中回弹，那么明日香会瞬间飞往相对高度$-8$。

如果使用一个重力粒子进行空中回弹，那么这个重力粒子将会立即消失，不能继续使用。重力粒子不会移动，彼此没有影响，明日香的移动也不影响重力粒子。

明日香是个强迫症，她必须清空场上所有的重力粒子。

在场外作为教练的你，已经观测到明日香所在空域的所有重力粒子的高度，需要指导明日香进行空中回弹所使用的重力粒子的顺序，让明日香飞得最高，即相对高度最大。

输入格式

第一行用空格分开的两个整数$n$和$a$表示有$n$个重力粒子，明日香在相对高度为$a$的位置上

第二行$n$个整数$h_i$表示第$i$个重力粒子的高度为$h_i$，对于任意$i<j$保证$h_i<h_j$

输出格式

一个整数$ans$，表示明日香的最高高度

样例1

输入

1 10
20

输出

30

样例2

输入

3 4
-5 2 5

输出

20

分别选中高度为2,-5,5的重力粒子进行空中回弹

数据范围

$1 \le n \le 10^{5}$

$-10^8\le a,h_i \le 10^8$

题解

方法一：数学分析

设当前明日香高度为$x$，重力粒子高度为$h$，接下来将要使用空中回弹飞行到$y=x+2*(h-x)$

即$y=-x+2h$

设$n$个$\{h_i\}$的一个排列为$\{a_i\}$，计算按$\{a_i\}$顺序空中回弹的最终高度$y_f$

$y_f=(-1)^n x+\sum_{i=0}^{n-1}(-1)^i *2a_i$

据排序不等式（或者贪心），只需将$n/2$个$-2$和$n-n/2$个$-2$组成向量，点乘上升序的$\{h_i\}$，加上$(-1)^n x$就是$y_f$的最大值

方法二：贪心

如果想让相对高度的绝对值最大，只需要每次使用距离明日香最远的重力粒子进行空中回弹即可。

不难发现如果第一次空中回弹使用在明日香上方最远的重力粒子，最终得到的高度是最高或最低。如果使用上方最远的重力粒子是最高，那么使用下方最远的重力粒子则是最低。如果下方是最低，使用上方是最高。

与$n$的奇偶性有关

即第一次空中回弹分别使用最上方的重力粒子和最下方的重力粒子，继续选择最远的重力粒子进行空中回弹，得到两个结果。取最大值即可。

不难证明和方法一等价。

std

#include <bits/stdc++.h>
using namespace std;
int main(){
	int n,a;
	cin>>n>>a;
	vector<long long> v(n);
	for (int i=0;i<n;i++)
		cin>>v[i];
	long long p=0;
	{
		int i;
		for (i=0;i<n/2;i++)
			p-=v[i]*2ll;
		for (;i<n;i++)
			p+=v[i]*2ll;
		p+=n%2?-a:a;
	}
	cout << p << endl;
	return 0;
}

[Ynoi2048] 这里没有数据结构

题面

题目背景

「抱歉……啦，羽依里……」

「你明明都没有抛弃我……」

「我却把你…你一个人留下了……」

「……那就是……我想要守护的东西啊……」

你要拯救的世界，要包括我吗?

"对于我来说，你就是地球的中心"

时间停止吧, 你是多么的美丽

……如今的鸟白岛上，已经不再有人会记住那个少女，还有她在这个夏天里，曾经在岛上四处奔走的那些事情。

但是，他们却都知道识的名字。

那挚爱的记忆，引领着未来。

题目描述

您正在推galgame，突然一把刀飞了过来，你抱头痛哭，准备做一道题缓解一下。

一个带重力的三维空间中，一个底朝正上方没有圆底面的圆锥型斗中即将分别放入液体和小球，小球半径和圆锥型斗的形状已知，请问液体和小球刚好接触时，液体的体积。

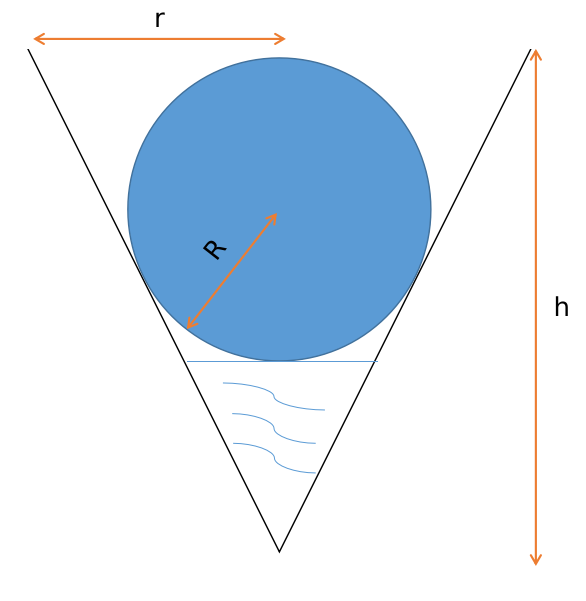横截面示意图

输入格式

三个空格隔开的整数$r,h,R$，分别表示圆锥形斗的圆底半径，圆锥形斗的高和小球的半径

输出格式

一个实数$a$，保留2位小数输出，表示小球和液体刚好接触时，液体的最大体积。

样例1

输入

5 5 5

输出

9.30

样例2

输入

5 5 100

输出

121.32

数据范围

$1\le r,h,R \le 10^2$

题解

灵感来源于今年一道XCPC/牛客多校签到题

数学

分两种情况，球和圆锥侧面相切和球和圆锥底面接触

得到球心到圆锥顶的距离，减去R即为液面高度

液面高度出来了，之后就算出来了（）

std

#include <bits/stdc++.h>

using namespace std;

int main(){
	double r,h,R;
	cin>>r>>h>>R;
	double b=R*h/r;
	double l=b<=sqrt(r*r+h*h)?
			 sqrt(b*b+R*R)-R:
			 sqrt(R*R-r*r)+h-R;
	double R2=r/h*l;
	cout << fixed << setprecision(2) << 
	M_PI*R2*R2*l/3 << endl;
}